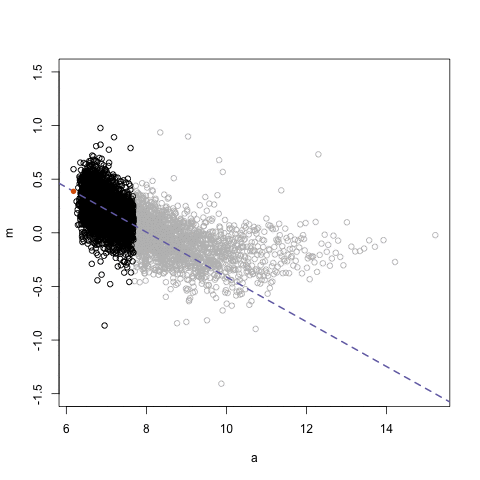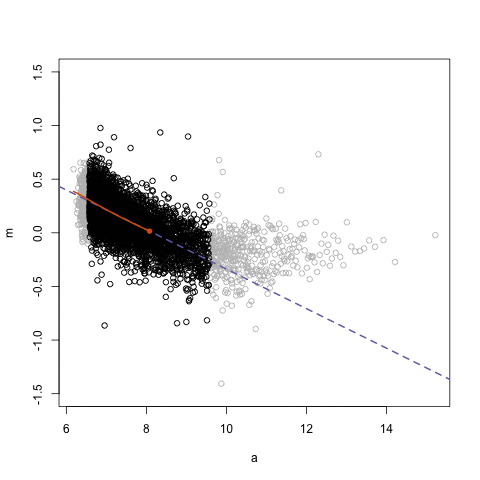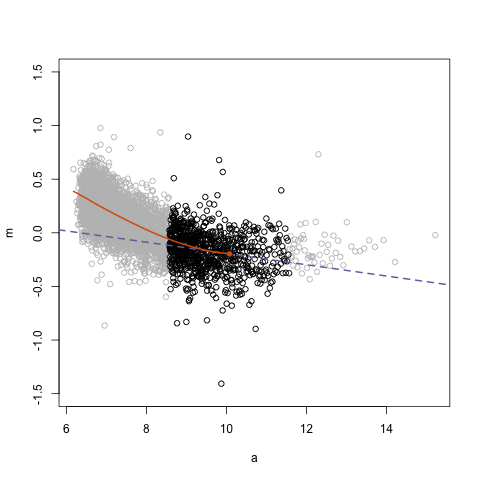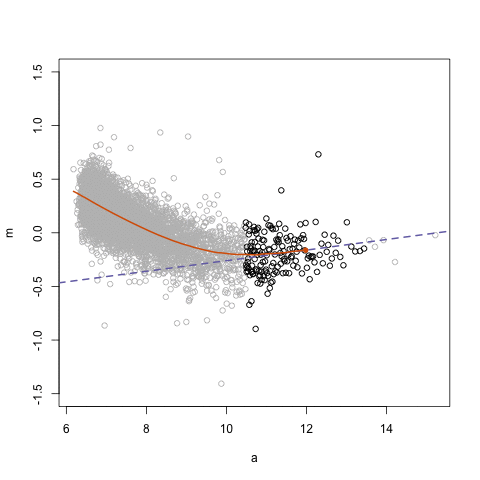
2 мӢңм°ЁмғҒкҙҖ(м„ н–ү, нӣ„н–ү) #
> tmp
curr_val prev_val
5 3949515 4316313
6 3835690 4149917
7 3975137 4165120
8 3993659 4050347
9 3942373 3949515
10 3825807 3835690
11 3920338 3975137
12 3586568 3993659
13 3633877 3942373
14 3444306 3825807
15 3903889 3920338
16 3529384 3586568
17 3531147 3633877
18 3518490 3444306
19 3481886 3903889
20 3298512 3529384
21 3400325 3531147
22 3641914 3518490
23 3466527 3481886
24 6028886 3298512
25 6543880 3400325
26 5516709 3641914
27 5100715 3466527
28 5259752 6028886
29 5370662 6543880
30 5009019 5516709
31 4778911 5100715
32 4836214 5259752
33 4662136 5370662
tmp <- na.omit(tmp)
ccf(tmp$curr_val, tmp$prev_val)
мІ« лІҲм§ё л§Өк°ңліҖмҲҳлҘј кё°мӨҖмңјлЎң м–јл§ҲлӮҳ м„ н–ү/нӣ„н–ү н•ҳлҠ”м§Җ м•Ң мҲҳ мһҲлӢӨ. к°ҖмһҘ ліјлЎқн•ҳкІҢ лӮҳмҳЁ л¶Җ분мқҙ x축м—җ -4 мқҙлӢҲк№Ң tmp$curr_valк°Җ лҢҖлһө 4мқјм •лҸ„ л№ лҘҙлӢӨ.
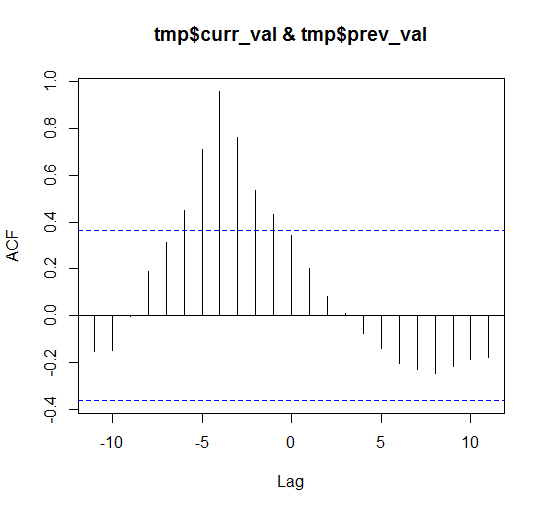
мІ« лІҲм§ё л§Өк°ңліҖмҲҳлҘј кё°мӨҖмңјлЎң м–јл§ҲлӮҳ м„ н–үн•ҳлҠ”м§Җ м•Ң мҲҳ мһҲлӢӨ.
lag.plot2(
 itall.R
itall.R) н•ЁмҲҳлҘј мқҙмҡ©н•ҙм„ң м°ЁнҠёлҘј к·ёл Өліҙмһҗ.
source("http://databaser.net/moniwiki/pds/TimeSeries/itall.R")
lag.plot2(tmp$curr_val , tmp$prev_val, 11)
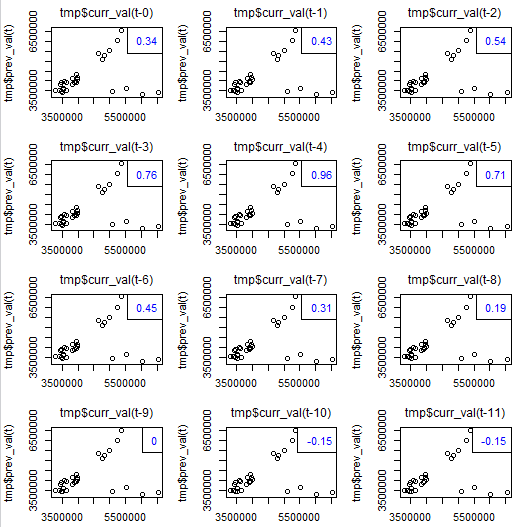
н‘ңмӨҖнҷ”н•ҙм„ң лқјмқё м°ЁнҠёлҘј к·ёл Өліҙмһҗ.
plot(scale(tmp$curr_val), type="l", col="red")
lines(scale(tmp$prev_val), col="blue")
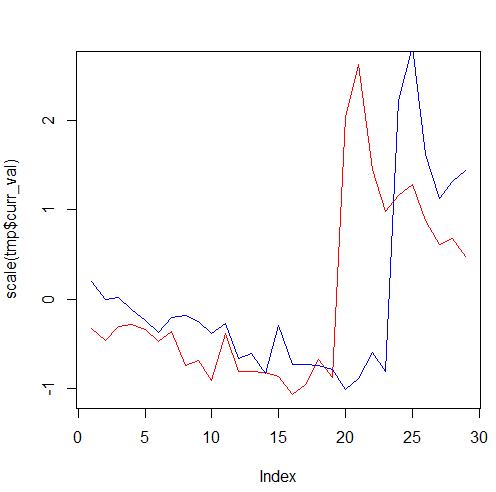
мөңлҢҖ/мөңмҶҢ көҗм°ЁмғҒкҙҖ л°Ҹ мӢңм°Ё (
![[http]](/moniwiki/imgs/http.png) м¶ңмІҳ(http://blog.naver.com/lofie21?Redirect=Log&logNo=110171809189)
м¶ңмІҳ(http://blog.naver.com/lofie21?Redirect=Log&logNo=110171809189))
max_ccf <- function(...)
{
d <- ccf(...)
cor <- d$acf[,,1]
lag <- d$lag[,,1]
dd <- data.frame(cor, lag)
max_val <- dd[which.max(dd$cor),]
min_val <- dd[which.min(dd$cor),]
result <- c()
if(abs(max_val[1]) >= abs(min_val[1])){
result <- max_val
} else {
result <- min_val
}
return(result)
}
max_ccf <- function(...)
{
d <- ccf(...)
cor <- d$acf[,,1]
lag <- d$lag[,,1]
df <- data.frame(cor, lag)
max_val <- df[which.max(df$cor),]
return(max_val)
}
min_ccf <- function(...)
{
d <- ccf(...)
cor <- d$acf[,,1]
lag <- d$lag[,,1]
df <- data.frame(cor, lag)
min_ccf <- df[which.min(df$cor),]
return(min_ccf)
}
мҳҲлҘј л“Өм–ҙ, лӢӨмқҢкіј к°ҷмқҙ кІ°кіјк°Җ лӮҳмҷ”лӢӨл©ҙ..
> max_ccf(sales, val)
cor lag
12 0.8932095 -1
- мөңлҢҖ мғҒкҙҖ кі„мҲҳлҠ” 0.89
- мӢң간축 мғҒм—җм„ң salesк°Җ valліҙлӢӨ -1мқј л’Өм ё мһҲмқҢмқ„ лң»н•Ё.
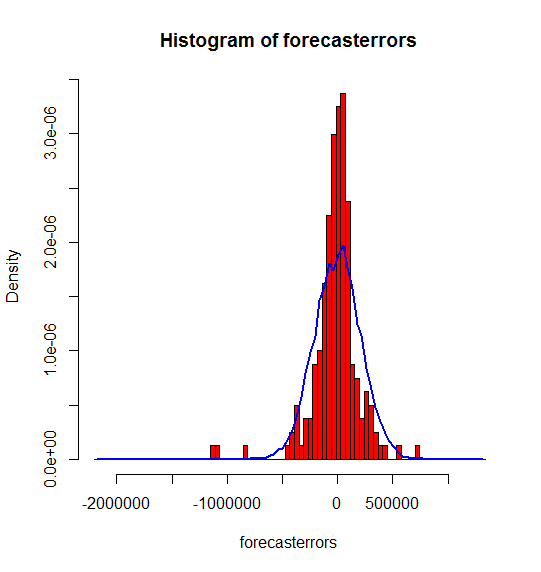
3 plotForecastErrors #
plotForecastErrors <- function(forecasterrors)
{
# make a histogram of the forecast errors:
mybinsize <- IQR(forecasterrors)/4
mysd <- sd(forecasterrors)
mymin <- min(forecasterrors) - mysd*5
mymax <- max(forecasterrors) + mysd*3
# generate normally distributed data with mean 0 and standard deviation mysd
mynorm <- rnorm(10000, mean=0, sd=mysd)
mymin2 <- min(mynorm)
mymax2 <- max(mynorm)
if (mymin2 < mymin) { mymin <- mymin2 }
if (mymax2 > mymax) { mymax <- mymax2 }
# make a red histogram of the forecast errors, with the normally distributed data overlaid:
mybins <- seq(mymin, mymax, mybinsize)
hist(forecasterrors, col="red", freq=FALSE, breaks=mybins)
# freq=FALSE ensures the area under the histogram = 1
# generate normally distributed data with mean 0 and standard deviation mysd
myhist <- hist(mynorm, plot=FALSE, breaks=mybins)
# plot the normal curve as a blue line on top of the histogram of forecast errors:
points(myhist$mids, myhist$density, type="l", col="blue", lwd=2)
}
p10 <- forecast(m, 10)
plotForecastErrors(p10 $residuals)
8 нҸүнҷң #
library("forecast")
data(gold)
g <- data.frame(g = na.omit(coredata(gold)))$g
y_width <- c(min(g) - min(g) * 0.05, max(g) - max(g) * 0.05)
plot(g, type="l", lty="dotted", ylim=y_width)
par(new=T)
plot(smooth(g, twiceit=T), type="l", col="blue", ylim=y_width, ylab="")
мқҙлҸҷмӨ‘к°„к°’ н•ЁмҲҳ : runmde()
![[http]](/moniwiki/imgs/http.png) л„ӨмқҙлІ„ көҗмңЎмҡ©м–ҙмӮ¬м „(http://terms.naver.com/entry.nhn?docId=1924236&cid=531&categoryId=531)
л„ӨмқҙлІ„ көҗмңЎмҡ©м–ҙмӮ¬м „(http://terms.naver.com/entry.nhn?docId=1924236&cid=531&categoryId=531)![[http]](/moniwiki/imgs/http.png) л„ӨмқҙлІ„ көҗмңЎмҡ©м–ҙмӮ¬м „(http://terms.naver.com/entry.nhn?docId=1924236&cid=531&categoryId=531)
л„ӨмқҙлІ„ көҗмңЎмҡ©м–ҙмӮ¬м „(http://terms.naver.com/entry.nhn?docId=1924236&cid=531&categoryId=531)