_대문 | 방명록 | 최근글 | 홈피소개 | 주인놈
FrontPage › MarkovChains
Data Analysis(R)
Data Analysis(Python)
Statistics
Data Warehouse
Database System
SQL Server
Trino
Hive
Hadoop
Regular Expressions
Tools
Money
Working Smart
Blog
Booklog
Philosophy
Link
Miscellaneous
__ edit




Contents

[-]
1 개요
2 마아코프 과정(markov process)
3 마아코프 분석의 전제
4 예제1: 신규서버 오픈
5 예제2: 일시상태, 재귀상태, 흡수상태
6 예제3: 종합병원 심장 치료 병동
7 예제4: 종합병원 심장 치료 병동 - markovchain packages
8 예제5: 데이터 프레임을 전이 확률로 만들기
9 예제6: 흡수상태가 포함된 전이행렬
10 HMM(Hidden Markov Model)
11 msm package
12 정말 이런 복잡한게 필요한가?
13 참고자료


[edit]

1 개요 #

  • 마아코프 분석은 확률적인 기법으로 결정 상황에 대한 확률적 정보만 제공한다. 즉, 서술적임
  • 어떤 시스템의 현재 상태를 분석하여 그 시스템의 미래의 상태를 예측함.
  • 시간의 흐름에 따른 상태 변화가 확률적으로 움직일 때에 사용함.
  • 브랜드명 교체, 인구이동, 인사 등

[edit]

2 마아코프 과정(markov process) #

  • 상태 S1에서 상태 S2로 변화할 때 확률이 적용되는 과정을 '확률적 가정(stochastic process)'라고 함.
  • 상태 S1에서 상태 S2로 변화할 때 S2가 S1에 의해 결정되는 확률적 가정은 '마아코프 과정(markov process)'라고 함.
  • 상태 S1에서 상태 S2로 변화할 때의 전이 확률(transition probablility)이 시간이 지났음에도 변화하지 않으면 '마아코프 체인(markov chain)'이라고 함.
  • 시간이 경과해도 상태 확률에 변화가 없으면 '안정상태(steady-state, long-run, equilibrium probablilty)' 라고 함.
    • 책에는 안정 상태를 계산하려고 연립방정식 풀고 그러는데, 그렇게 안해도 그냥 100단계, 1000단계로 돌리면 확인할 수 있다.
[edit]

3 마아코프 분석의 전제 #

  • 시스템은 유한한 수의 상태를 가진다.
  • 시스템은 여러 기간 동안 존재한다.
  • 각 기간에 있어 시스템은 한 상태에 속한다.
  • 각 상태는 상호배타적이다.
  • 전이 확률은 시간이 경과해도 일정하다.
  • 특정 기간의 상태는 바로 전의 상태와 전이확률에 의존한다.
  • 상태변화는 각 기간에 한 번만 발생한다.
  • 각 기간은 길이가 일정하다.
  • 마아코프 분석은 현재의 시초 상황에서 시작한다.

[edit]

4 예제1: 신규서버 오픈 #

  • B서버(게임)를 새로 오픈했다. 이전에 신규 서버 오픈시의 일단위의 고객의 이동에 대한 전이 확률을 조사해봤더니 다음과 같더라.
    • 구서버 -> 구서버: 0.9
    • 구서버 -> 신서버: 0.1
    • 신서버 -> 구서버: 0.3
    • 구서버 -> 구서버: 0.7
  • 처음에 A서버에서 100명이 이용하고 있었다. (일단은 골치 아프니 신규가입은 없다고 가정하자)
  • 22일차 정도면 안정상태가 되고, 구서버에는 75명, 신서버에는 25명이 된다고 예측할 수 있다.

x1 <- c(0.9, 0.1)
x2 <- c(0.3, 0.7)
tp <- rbind(x1, x2) #전이확률
ss <- rbind(c(100,0)) #시초

for(t in seq(1:30)){
  
  prev_tp <- ss%*%tp
  out <- paste(t, "일차: ", "구서버:", round(prev_tp[1,1], 3), "신서버:", round(prev_tp[1,2], 3))
  ss <- prev_tp
  print (out)
}

결과
[1] "1 일차:  구서버: 90 신서버: 10"
[1] "2 일차:  구서버: 84 신서버: 16"
[1] "3 일차:  구서버: 80.4 신서버: 19.6"
[1] "4 일차:  구서버: 78.24 신서버: 21.76"
[1] "5 일차:  구서버: 76.944 신서버: 23.056"
[1] "6 일차:  구서버: 76.166 신서버: 23.834"
[1] "7 일차:  구서버: 75.7 신서버: 24.3"
[1] "8 일차:  구서버: 75.42 신서버: 24.58"
[1] "9 일차:  구서버: 75.252 신서버: 24.748"
[1] "10 일차:  구서버: 75.151 신서버: 24.849"
[1] "11 일차:  구서버: 75.091 신서버: 24.909"
[1] "12 일차:  구서버: 75.054 신서버: 24.946"
[1] "13 일차:  구서버: 75.033 신서버: 24.967"
[1] "14 일차:  구서버: 75.02 신서버: 24.98"
[1] "15 일차:  구서버: 75.012 신서버: 24.988"
[1] "16 일차:  구서버: 75.007 신서버: 24.993"
[1] "17 일차:  구서버: 75.004 신서버: 24.996"
[1] "18 일차:  구서버: 75.003 신서버: 24.997"
[1] "19 일차:  구서버: 75.002 신서버: 24.998"
[1] "20 일차:  구서버: 75.001 신서버: 24.999"
[1] "21 일차:  구서버: 75.001 신서버: 24.999"
[1] "22 일차:  구서버: 75 신서버: 25"
[1] "23 일차:  구서버: 75 신서버: 25"
[1] "24 일차:  구서버: 75 신서버: 25"
[1] "25 일차:  구서버: 75 신서버: 25"
[1] "26 일차:  구서버: 75 신서버: 25"
[1] "27 일차:  구서버: 75 신서버: 25"
[1] "28 일차:  구서버: 75 신서버: 25"
[1] "29 일차:  구서버: 75 신서버: 25"
[1] "30 일차:  구서버: 75 신서버: 25"

[edit]

5 예제2: 일시상태, 재귀상태, 흡수상태 #

만약 예제1에서 신서버에서 구서버로 이동이 없다고 가정하면, 116일차에 안정상태에 돌입한다. 즉, 구서버에 사람이 한명도 남지 않게 된다고 예측 할 수 있다. 이런 상태를 '일시 상태(transient state)'라고 한다. 일시 상태가 아닌 예제1과 같은 상태를 '재귀 상태(recurrent state)'라고 하며, 재귀 상태 중 안정 상태를 '흡수 상태(absorbing state)'라고 한다. 흡수 상태는 시스템이 궁극적으로 도달하는 상태이므로 현실적으로 중요한 의미를 갖는 경우가 많다. (라고 [http]여기에서 그러더라)

x1 <- c(0.9, 0.1)
x2 <- c(0.0, 1.0)
tp <- rbind(x1, x2) #전이확률
ss <- rbind(c(100,0)) #시초

for(t in seq(1:120)){
  
  prev_tp <- ss%*%tp
  out <- paste(t, "일차: ", "구서버:", round(prev_tp[1,1], 3), "신서버:", round(prev_tp[1,2], 3))
  ss <- prev_tp
  print (out)
}

[1] "1 일차:  구서버: 90 신서버: 10"
[1] "2 일차:  구서버: 81 신서버: 19"
[1] "3 일차:  구서버: 72.9 신서버: 27.1"
[1] "4 일차:  구서버: 65.61 신서버: 34.39"
[1] "5 일차:  구서버: 59.049 신서버: 40.951"
[1] "6 일차:  구서버: 53.144 신서버: 46.856"
[1] "7 일차:  구서버: 47.83 신서버: 52.17"
[1] "8 일차:  구서버: 43.047 신서버: 56.953"
[1] "9 일차:  구서버: 38.742 신서버: 61.258"
[1] "10 일차:  구서버: 34.868 신서버: 65.132"
[1] "11 일차:  구서버: 31.381 신서버: 68.619"
[1] "12 일차:  구서버: 28.243 신서버: 71.757"
[1] "13 일차:  구서버: 25.419 신서버: 74.581"
[1] "14 일차:  구서버: 22.877 신서버: 77.123"
[1] "15 일차:  구서버: 20.589 신서버: 79.411"
[1] "16 일차:  구서버: 18.53 신서버: 81.47"
[1] "17 일차:  구서버: 16.677 신서버: 83.323"
[1] "18 일차:  구서버: 15.009 신서버: 84.991"
[1] "19 일차:  구서버: 13.509 신서버: 86.491"
[1] "20 일차:  구서버: 12.158 신서버: 87.842"
[1] "21 일차:  구서버: 10.942 신서버: 89.058"
[1] "22 일차:  구서버: 9.848 신서버: 90.152"
[1] "23 일차:  구서버: 8.863 신서버: 91.137"
[1] "24 일차:  구서버: 7.977 신서버: 92.023"
[1] "25 일차:  구서버: 7.179 신서버: 92.821"
[1] "26 일차:  구서버: 6.461 신서버: 93.539"
[1] "27 일차:  구서버: 5.815 신서버: 94.185"
[1] "28 일차:  구서버: 5.233 신서버: 94.767"
[1] "29 일차:  구서버: 4.71 신서버: 95.29"
[1] "30 일차:  구서버: 4.239 신서버: 95.761"
[1] "31 일차:  구서버: 3.815 신서버: 96.185"
[1] "32 일차:  구서버: 3.434 신서버: 96.566"
[1] "33 일차:  구서버: 3.09 신서버: 96.91"
[1] "34 일차:  구서버: 2.781 신서버: 97.219"
[1] "35 일차:  구서버: 2.503 신서버: 97.497"
[1] "36 일차:  구서버: 2.253 신서버: 97.747"
[1] "37 일차:  구서버: 2.028 신서버: 97.972"
[1] "38 일차:  구서버: 1.825 신서버: 98.175"
[1] "39 일차:  구서버: 1.642 신서버: 98.358"
[1] "40 일차:  구서버: 1.478 신서버: 98.522"
[1] "41 일차:  구서버: 1.33 신서버: 98.67"
[1] "42 일차:  구서버: 1.197 신서버: 98.803"
[1] "43 일차:  구서버: 1.078 신서버: 98.922"
[1] "44 일차:  구서버: 0.97 신서버: 99.03"
[1] "45 일차:  구서버: 0.873 신서버: 99.127"
[1] "46 일차:  구서버: 0.786 신서버: 99.214"
[1] "47 일차:  구서버: 0.707 신서버: 99.293"
[1] "48 일차:  구서버: 0.636 신서버: 99.364"
[1] "49 일차:  구서버: 0.573 신서버: 99.427"
[1] "50 일차:  구서버: 0.515 신서버: 99.485"
[1] "51 일차:  구서버: 0.464 신서버: 99.536"
[1] "52 일차:  구서버: 0.417 신서버: 99.583"
[1] "53 일차:  구서버: 0.376 신서버: 99.624"
[1] "54 일차:  구서버: 0.338 신서버: 99.662"
[1] "55 일차:  구서버: 0.304 신서버: 99.696"
[1] "56 일차:  구서버: 0.274 신서버: 99.726"
[1] "57 일차:  구서버: 0.247 신서버: 99.753"
[1] "58 일차:  구서버: 0.222 신서버: 99.778"
[1] "59 일차:  구서버: 0.2 신서버: 99.8"
[1] "60 일차:  구서버: 0.18 신서버: 99.82"
[1] "61 일차:  구서버: 0.162 신서버: 99.838"
[1] "62 일차:  구서버: 0.146 신서버: 99.854"
[1] "63 일차:  구서버: 0.131 신서버: 99.869"
[1] "64 일차:  구서버: 0.118 신서버: 99.882"
[1] "65 일차:  구서버: 0.106 신서버: 99.894"
[1] "66 일차:  구서버: 0.096 신서버: 99.904"
[1] "67 일차:  구서버: 0.086 신서버: 99.914"
[1] "68 일차:  구서버: 0.077 신서버: 99.923"
[1] "69 일차:  구서버: 0.07 신서버: 99.93"
[1] "70 일차:  구서버: 0.063 신서버: 99.937"
[1] "71 일차:  구서버: 0.056 신서버: 99.944"
[1] "72 일차:  구서버: 0.051 신서버: 99.949"
[1] "73 일차:  구서버: 0.046 신서버: 99.954"
[1] "74 일차:  구서버: 0.041 신서버: 99.959"
[1] "75 일차:  구서버: 0.037 신서버: 99.963"
[1] "76 일차:  구서버: 0.033 신서버: 99.967"
[1] "77 일차:  구서버: 0.03 신서버: 99.97"
[1] "78 일차:  구서버: 0.027 신서버: 99.973"
[1] "79 일차:  구서버: 0.024 신서버: 99.976"
[1] "80 일차:  구서버: 0.022 신서버: 99.978"
[1] "81 일차:  구서버: 0.02 신서버: 99.98"
[1] "82 일차:  구서버: 0.018 신서버: 99.982"
[1] "83 일차:  구서버: 0.016 신서버: 99.984"
[1] "84 일차:  구서버: 0.014 신서버: 99.986"
[1] "85 일차:  구서버: 0.013 신서버: 99.987"
[1] "86 일차:  구서버: 0.012 신서버: 99.988"
[1] "87 일차:  구서버: 0.01 신서버: 99.99"
[1] "88 일차:  구서버: 0.009 신서버: 99.991"
[1] "89 일차:  구서버: 0.008 신서버: 99.992"
[1] "90 일차:  구서버: 0.008 신서버: 99.992"
[1] "91 일차:  구서버: 0.007 신서버: 99.993"
[1] "92 일차:  구서버: 0.006 신서버: 99.994"
[1] "93 일차:  구서버: 0.006 신서버: 99.994"
[1] "94 일차:  구서버: 0.005 신서버: 99.995"
[1] "95 일차:  구서버: 0.004 신서버: 99.996"
[1] "96 일차:  구서버: 0.004 신서버: 99.996"
[1] "97 일차:  구서버: 0.004 신서버: 99.996"
[1] "98 일차:  구서버: 0.003 신서버: 99.997"
[1] "99 일차:  구서버: 0.003 신서버: 99.997"
[1] "100 일차:  구서버: 0.003 신서버: 99.997"
[1] "101 일차:  구서버: 0.002 신서버: 99.998"
[1] "102 일차:  구서버: 0.002 신서버: 99.998"
[1] "103 일차:  구서버: 0.002 신서버: 99.998"
[1] "104 일차:  구서버: 0.002 신서버: 99.998"
[1] "105 일차:  구서버: 0.002 신서버: 99.998"
[1] "106 일차:  구서버: 0.001 신서버: 99.999"
[1] "107 일차:  구서버: 0.001 신서버: 99.999"
[1] "108 일차:  구서버: 0.001 신서버: 99.999"
[1] "109 일차:  구서버: 0.001 신서버: 99.999"
[1] "110 일차:  구서버: 0.001 신서버: 99.999"
[1] "111 일차:  구서버: 0.001 신서버: 99.999"
[1] "112 일차:  구서버: 0.001 신서버: 99.999"
[1] "113 일차:  구서버: 0.001 신서버: 99.999"
[1] "114 일차:  구서버: 0.001 신서버: 99.999"
[1] "115 일차:  구서버: 0.001 신서버: 99.999"
[1] "116 일차:  구서버: 0 신서버: 100"
[1] "117 일차:  구서버: 0 신서버: 100"
[1] "118 일차:  구서버: 0 신서버: 100"
[1] "119 일차:  구서버: 0 신서버: 100"
[1] "120 일차:  구서버: 0 신서버: 100"

[edit]

6 예제3: 종합병원 심장 치료 병동 #

예제출처: http://secom.hanbat.ac.kr/or/chapter1/right04.html
어느 종합병원의 심장병 치료 특수병동에 입원중인 환자는 환자의 상태에 따라 일반병동으로 이동하거나 퇴원하는데, 퇴원하는 경우 중 85%는 치료되어 퇴원하며 15%는 사망하는 경우이다. 치료되어 퇴원한 환자중 일부는 새로운 환자로서 다시 입원하기도 하며 치료대상인 심장병환자의 수가 일정하고, 1일 전이확률이 아래의 표와 같다고 한다.

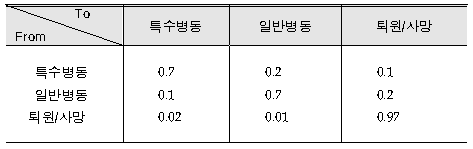
chapter1-17.gif

x1 <- c(0.7, 0.2, 0.1)
x2 <- c(0.1, 0.7, 0.2)
x3 <- c(0.02, 0.01, 0.97)
tp <- rbind(x1, x2, x3) #전이확률
ss <- rbind(c(1,0,0)) #시초

for(t in seq(1:50)){
  
  prev_tp <- ss%*%tp
  out <- paste(t, "일차: ", 
               "특수병동:", round(prev_tp[1,1], 3), 
               "일반병동:", round(prev_tp[1,2], 3),
               "퇴원/사망:", round(prev_tp[1,3], 3)
               )
  ss <- prev_tp
  print (out)
}

결과
[1] "1 일차:  특수병동: 0.7 일반병동: 0.2 퇴원/사망: 0.1"
[1] "2 일차:  특수병동: 0.512 일반병동: 0.281 퇴원/사망: 0.207"
[1] "3 일차:  특수병동: 0.391 일반병동: 0.301 퇴원/사망: 0.308"
[1] "4 일차:  특수병동: 0.31 일반병동: 0.292 퇴원/사망: 0.398"
[1] "5 일차:  특수병동: 0.254 일반병동: 0.27 퇴원/사망: 0.476"
[1] "6 일차:  특수병동: 0.214 일반병동: 0.245 퇴원/사망: 0.541"
[1] "7 일차:  특수병동: 0.185 일반병동: 0.22 퇴원/사망: 0.595"
[1] "8 일차:  특수병동: 0.164 일반병동: 0.197 퇴원/사망: 0.64"
[1] "9 일차:  특수병동: 0.147 일반병동: 0.177 퇴원/사망: 0.676"
[1] "10 일차:  특수병동: 0.134 일반병동: 0.16 퇴원/사망: 0.706"
[1] "11 일차:  특수병동: 0.124 일반병동: 0.146 퇴원/사망: 0.73"
[1] "12 일차:  특수병동: 0.116 일반병동: 0.134 퇴원/사망: 0.75"
[1] "13 일차:  특수병동: 0.11 일반병동: 0.125 퇴원/사망: 0.766"
[1] "14 일차:  특수병동: 0.104 일반병동: 0.117 퇴원/사망: 0.779"
[1] "15 일차:  특수병동: 0.1 일반병동: 0.11 퇴원/사망: 0.789"
[1] "16 일차:  특수병동: 0.097 일반병동: 0.105 퇴원/사망: 0.798"
[1] "17 일차:  특수병동: 0.094 일반병동: 0.101 퇴원/사망: 0.804"
[1] "18 일차:  특수병동: 0.092 일반병동: 0.098 퇴원/사망: 0.81"
[1] "19 일차:  특수병동: 0.091 일반병동: 0.095 퇴원/사망: 0.814"
[1] "20 일차:  특수병동: 0.089 일반병동: 0.093 퇴원/사망: 0.818"
[1] "21 일차:  특수병동: 0.088 일반병동: 0.091 퇴원/사망: 0.821"
[1] "22 일차:  특수병동: 0.087 일반병동: 0.089 퇴원/사망: 0.823"
[1] "23 일차:  특수병동: 0.086 일반병동: 0.088 퇴원/사망: 0.825"
[1] "24 일차:  특수병동: 0.086 일반병동: 0.087 퇴원/사망: 0.827"
[1] "25 일차:  특수병동: 0.085 일반병동: 0.087 퇴원/사망: 0.828"
[1] "26 일차:  특수병동: 0.085 일반병동: 0.086 퇴원/사망: 0.829"
[1] "27 일차:  특수병동: 0.085 일반병동: 0.085 퇴원/사망: 0.83"
[1] "28 일차:  특수병동: 0.084 일반병동: 0.085 퇴원/사망: 0.831"
[1] "29 일차:  특수병동: 0.084 일반병동: 0.085 퇴원/사망: 0.831"
[1] "30 일차:  특수병동: 0.084 일반병동: 0.084 퇴원/사망: 0.832"
[1] "31 일차:  특수병동: 0.084 일반병동: 0.084 퇴원/사망: 0.832"
[1] "32 일차:  특수병동: 0.084 일반병동: 0.084 퇴원/사망: 0.832"
[1] "33 일차:  특수병동: 0.084 일반병동: 0.084 퇴원/사망: 0.832"
[1] "34 일차:  특수병동: 0.084 일반병동: 0.084 퇴원/사망: 0.833"
[1] "35 일차:  특수병동: 0.084 일반병동: 0.084 퇴원/사망: 0.833"
[1] "36 일차:  특수병동: 0.084 일반병동: 0.084 퇴원/사망: 0.833"
[1] "37 일차:  특수병동: 0.083 일반병동: 0.084 퇴원/사망: 0.833"
[1] "38 일차:  특수병동: 0.083 일반병동: 0.084 퇴원/사망: 0.833"
[1] "39 일차:  특수병동: 0.083 일반병동: 0.083 퇴원/사망: 0.833"
[1] "40 일차:  특수병동: 0.083 일반병동: 0.083 퇴원/사망: 0.833"
[1] "41 일차:  특수병동: 0.083 일반병동: 0.083 퇴원/사망: 0.833"
[1] "42 일차:  특수병동: 0.083 일반병동: 0.083 퇴원/사망: 0.833"
[1] "43 일차:  특수병동: 0.083 일반병동: 0.083 퇴원/사망: 0.833"
[1] "44 일차:  특수병동: 0.083 일반병동: 0.083 퇴원/사망: 0.833"
[1] "45 일차:  특수병동: 0.083 일반병동: 0.083 퇴원/사망: 0.833"
[1] "46 일차:  특수병동: 0.083 일반병동: 0.083 퇴원/사망: 0.833"
[1] "47 일차:  특수병동: 0.083 일반병동: 0.083 퇴원/사망: 0.833"
[1] "48 일차:  특수병동: 0.083 일반병동: 0.083 퇴원/사망: 0.833"
[1] "49 일차:  특수병동: 0.083 일반병동: 0.083 퇴원/사망: 0.833"
[1] "50 일차:  특수병동: 0.083 일반병동: 0.083 퇴원/사망: 0.833"
심장병환자의 8.3%씩이 각각 특수병동과 일반병동에서 치료중이며 83.34%는 사망하였거나 치료되어 퇴원한 상태라고 추정할 수 있다.

[edit]

7 예제4: 종합병원 심장 치료 병동 - markovchain packages #

http://cran.r-project.org/web/packages/markovchain/markovchain.pdf
install.packages("markovchain")
library("markovchain")

statesNames=c("특수병동","일반병동", "퇴원/사망")
mt <- matrix(c(0.7,0.2,0.1,0.1,0.7,0.2,0.02,0.01,0.97), byrow=TRUE, nrow=3)
mc<-new("markovchain", transitionMatrix=mt, states=statesNames)
mc^2 #2번째 단계
steadyStates(mc)

결과
> mc^2
A Markov chain^2 
 A  3 - dimensional discrete Markov Chain with following states 
 특수병동 일반병동 퇴원/사망 
 The transition matrix   (by rows)  is defined as follows 
          특수병동 일반병동 퇴원/사망
특수병동    0.5120   0.2810    0.2070
일반병동    0.1440   0.5120    0.3440
퇴원/사망   0.0344   0.0207    0.9449

> steadyStates(mcA)
       특수병동   일반병동 퇴원/사망
[1,] 0.08333333 0.08333333 0.8333333
[edit]

8 예제5: 데이터 프레임을 전이 확률로 만들기 #

raw <- data.frame(name=c("f1","f1","f1","f1","f2","f2","f2","f2"),
                  year=c(83,   84,  85,  86,  83,  84,  85,  86),
                  state=sample(1:3, 8, replace=TRUE)
                  )

transition.probabilities <- function(D, timevar="year",
                                     idvar="name", statevar="state") {
  merged <- merge(D, cbind(nextt=D[,timevar] + 1, D),
    by.x = c(timevar, idvar), by.y = c("nextt", idvar))
  t(table(merged[, grep(statevar, names(merged), value = TRUE)]))
}

transition.probabilities(raw, timevar="year", idvar="name",statevar="state")


install.packages("markovchain")
library("markovchain")

sequence<-c("a", "b", "a", "a", "a", "a", "b", "a", "b", "a", "b", "a", "a", "b", "b", "b", "a")
mcFitMLE<-markovchainFit(data=sequence)
#str(mcFitMLE)
#mcFitMLE$estimate@transitionMatrix
#mcFitMLE$estimate@states
markov<-new("markovchain", states=mcFitMLE$estimate@states, transitionMatrix=mcFitMLE$estimate@transitionMatrix)
plotMc(markov)

[edit]

9 예제6: 흡수상태가 포함된 전이행렬 #

D백화점 1,000고객의 신용계정 상태(http://secom.hanbat.ac.kr/or/chapter1/right04.html)
1.png
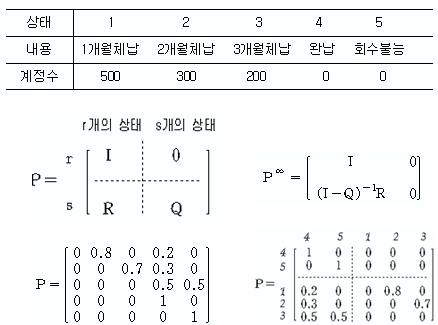
R <- matrix(c(0.2,0, 0.3,0,0.5,0.5), byrow=TRUE, nrow=3)
Q <- matrix(c(0,0.8,0,0,0,0.7,0,0,0), byrow=TRUE, nrow=3)
IQ <- diag(rep(1,3)) - Q
IQ
iIQ<-ginv(IQ)
iIQ %*% R
rowSums(iIQ)

[edit]

10 HMM(Hidden Markov Model) #

  • 마코프 모델에 '은닉'이라는 개념을 추가
  • 스칼라 & 이산 이어야 함.

예제: 패턴인식 p.244, 오일석
날씨의 전이 행렬이 다음과 같다.
비해
비0.70.3
해0.40.6

초기 상태 확률은
  • 비 = 0.6
  • 해 = 0.4

날씨에 따라 하는 일
  • 비
    • 산책 = 0.1
    • 쇼핑 = 0.4
    • 청소 = 0.5
  • 해
    • 산책 = 0.6
    • 쇼핑 = 0.3
    • 청소 = 0.1

'산책->산책->청소->쇼핑' 을 했다면 각각의 날에 예측되는 날씨는?
#install.packages("RHmm")
library("RHmm")

weatherTransitions <- 
  rbind(
    c(0.7, 0.3),
    c(0.4, 0.6)
  )

s1 <- c(0.1, 0.4, 0.5)
s2 <- c(0.6, 0.3, 0.1)
dist <- distributionSet(dis="DISCRETE", proba=list(s1, s2), labels =c("산책", "쇼핑", "청소"))
dist

weatherHmm <- HMMSet(initProb=c(0.6, 0.4), transMat=weatherTransitions, distribution=dist)
weatherPath <- viterbi(HMM=weatherHmm, obs=c("산책", "산책", "청소", "쇼핑"))
weatherPath

결과
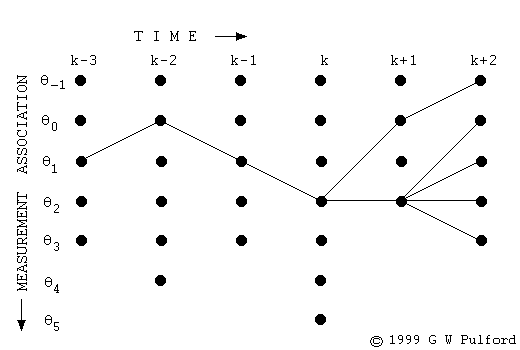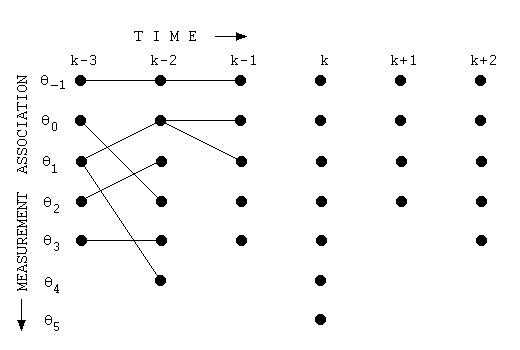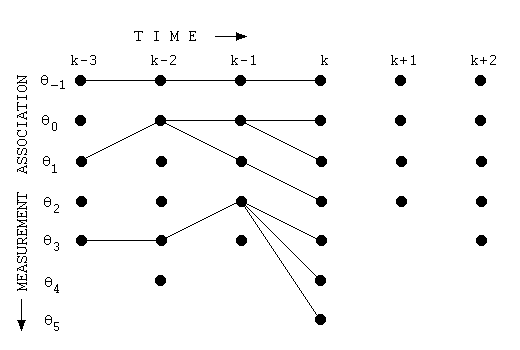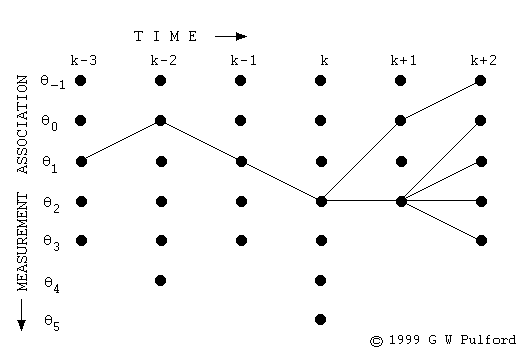
> weatherPath
$states
[1] 2 2 1 1

$logViterbiScore
[1] -5.331171

$logProbSeq
[1] -0.8306799

attr(,"class")
[1] "viterbiClass"
>
  • states가 2 2 1 1로 '해->해->비->비' 였을 가능성이 제일 크다.
  • '산책->산책->청소->쇼핑'의 최적 상태열의 값(viterbi score)은 0.0048384다. (exp(weatherPath$logViterbiScore))
  • '산책->산책->청소->쇼핑'의 발생 확률은 0.4357529 (exp(weatherPath$logProbSeq)) --> 맞나??

질문들
  • 그녀가 일주일 연속으로 쇼핑만 할 확률은?
  • '산책->산책->청소'를 한 경우 3일간의 날씨는?
  • 지난 3일 동안 '산책->산책->청소'를 했는데, 오늘과 내일은 무엇을 할 것으로 예측되나?

참고:viterbi 알고리즘
viterbi.gif

[edit]

11 msm package #

library("msm")
data("cav")
str(cav)
cav <- cav[!is.na(cav$pdiag),]
cav[1:11,]

m <- statetable.msm(state, PTNUM, data = cav)
class(m)

twoway4.q <- rbind(c(0, 0.25, 0, 0.25), 
                    c(0.166, 0, 0.166, 0.166), 
                    c(0, 0.25, 0, 0.25), 
                    c(0, 0, 0, 0))
rownames(twoway4.q) <- colnames(twoway4.q) <- c("Well", "Mild", "Severe", "Death")

cav.msm <- msm(state ~ years, subject = PTNUM, data = cav, qmatrix = twoway4.q, death = 4)
#pmatrix.msm(cav.msm, t = 1, ci = "normal")
pmatrix.msm(cav.msm, t = 1, ci = "none")


> pmatrix.msm(cav.msm, t = 1, ci = "none")
              Well       Mild     Severe      Death
Well   0.853040629 0.08916579 0.01486643 0.04292715
Mild   0.156269251 0.56585635 0.20550354 0.07237086
Severe 0.009996569 0.07884756 0.66057662 0.25057925
Death  0.000000000 0.00000000 0.00000000 1.00000000

[edit]

12 정말 이런 복잡한게 필요한가? #

고객이 100만 명이 있다. 고객들을 가입,구매,이탈에 대해 추적해 봤으며, 다음과 같은 패턴을 보였다.

패턴비율
가입50%
가입->이탈30%
가입->구매->구매->이탈10%
가입->구매5%
가입->구매->이탈3%
가입->구매->구매->구매2%

'가입->구매->?' 물음표(?)는 무엇이겠는가? 당연히 '구매'일 확률이 높지 않겠는가?
음..데이터 분석에서는 마코프 모델이 필요하지 않을 수도 있겠다.



댓글 남기기..
이름: : 오른쪽의 새로고침을 클릭해 주세요. 새로고침
EditText : Print : Mobile : FindPage : DeletePage : LikePages : Powered by MoniWiki : Last modified 2018-04-13 23:12:53

야구심판은 잘 하고 있을 때는 있는지 없는 지 모른다. (박경호)