[edit]
1 요인분석 개요 #
요인의 종류
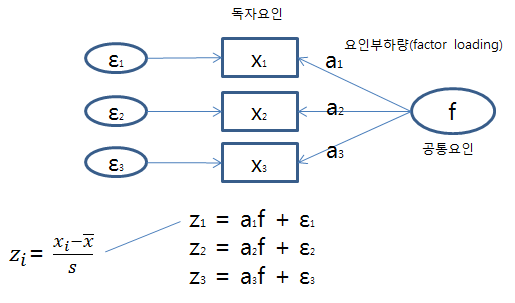
- 공통요인(common factor) - 관측할 수 없는 것으로 가정
- 독자요인(unique factor)
- 변수간에 높은 상관관계가 있어야 함.
- 최초 요인 추출 단계에서 얻은 고유치를 스크리 차트로 표시했을 때 한 군데 이상 꺽이는 곳이 있어야 함.
- 모상관 행렬이 단위 행렬이라는 가설이 기각되어야 함. (KMO and Bartleet's 검정)
- 탐색적 요인 분석: 변수 압축이 목적(주성분분석, 주요인분석, 최대우도요인분석 ...)
- 확인적 요인 분석: 어떤 가설이나 모델의 검증이 목적
- 변수간의 상관행렬로부터 공통요인을 도출
- 도출된 공통요인을 이용해서 변수간의 상관관계를 설명
- 요인부하량(factor loading)은 ±0.3 이상이면 유의하다고 봄.
- 공통요인과의 관계에 의해서 각 변수의 성질을 간결한 형태로 기술
- 요인분석 결과를 변수나 관측대상의 분류를 위해서 사용

요인의 해석
이건 비즈니스 종속적으로 요인분석이 나오는거 보고 주관적으로 해석된다.
이건 비즈니스 종속적으로 요인분석이 나오는거 보고 주관적으로 해석된다.
용도
- 정보의 요약(주성분 분석과 비슷)
- 변수들 내부에 존재하는 구조 발견
- 요인으로 묶이지 않는 중요도가 낮은 변수 제거
- 같은 개념을 측정하는 변수들이 동일한 요인으로 묶이는지 확인
- 회귀분석이나 판별분석의 설명변수 선택
- 요인과 변수들 사이의 관계를 해석하기 어려운 경우 요인적재값의 절대값을 0 또는 1에 가까워지도록 요인들의 축을 회전시키는 것.
- 직각회전(orthogonal rotation)
- 요인들간의 관계가 독립(상관관계 0)으로 간주할 때 사용(회귀분석이나 판별분석다 다중공선성을 피하기 위해서도 사용)
- varimax, quartimax, equimax
- 요인들간의 관계가 독립(상관관계 0)으로 간주할 때 사용(회귀분석이나 판별분석다 다중공선성을 피하기 위해서도 사용)
- 사각회전(oblique rotation)
- 사회과학에서는 대부분 이걸 사용한다. 왜냐하면 요인들간의 관계가 독립인 것이 별로 없다고 보기 때문.
- 직각회전 방식에 비해 높은 요인부하량은 더 높아지고, 낮은 부하량은 더 낮아짐
- oblimin, covarimin, quartimin, biquartimin, promax
- 사회과학에서는 대부분 이걸 사용한다. 왜냐하면 요인들간의 관계가 독립인 것이 별로 없다고 보기 때문.
- R의 factanal 에서는 varimax, promax만 지원, 더 많은 rotation을 지원하려면 GPArotation 패키지 설치하면 된다고 한다.
[edit]
2 요인의 level 조정 #
> x <- c("5천", "5만")
> x <- factor(x)
> x
[1] 5천 5만
Levels: 5만 5천
> levels(x) <- c("5천", "5만")
> x
[1] 5만 5천
Levels: 5천 5만
[edit]
3 R #
테스트 데이터는 "Excel에 의한 조사방법 및 통계분석, 노형진, 한울"의 예제다.
tmp <- textConnection( "청결상태 음식량 대기시간 음식맛 친절 6 4 7 6 5 5 7 5 6 6 5 3 4 5 6 3 3 2 3 4 4 3 3 3 2 2 6 2 4 3 1 3 3 3 2 3 5 3 4 2 7 3 6 5 5 6 4 3 4 4 6 6 3 6 4 3 2 2 4 2 5 7 2 5 2 6 3 6 5 7 3 4 5 3 2 2 7 5 5 4 3 5 2 7 2 6 4 5 5 7 7 4 6 3 5 5 6 6 3 4 2 3 3 4 3 3 4 2 3 4 3 6 3 5 3 6 5 7 5 5 7 6 5 4 6") x <- read.table(tmp, header=TRUE) close.connection(tmp) #head(x)
먼저 주성분분석과 요인분석의 차이를 보자.
#install.packages("psych")
#library("psych")
fa.parallel(x)
결과
> fa.parallel(x) Parallel analysis suggests that the number of factors = 2 and the number of components = 2요인이 2개라고 추천해줬다.

- 주성분 분석은 제5주성분까지 유의미
- 요인 분석은 2요인까지로 축소 --> 요걸로 함.
fit <- factanal(x, 2, rotation="promax") print(fit) #print(fit, cutoff = 1e-05, digits = 2)
결과
> print(fit)
Call:
factanal(x = x, factors = 2, rotation = "promax")
Uniquenesses:
청결상태 음식량 대기시간 음식맛 친절
0.339 0.869 0.419 0.005 0.287
Loadings:
Factor1 Factor2
청결상태 0.801
음식량 0.371
대기시간 0.775
음식맛 0.988
친절 0.833
Factor1 Factor2
SS loadings 1.939 1.122
Proportion Var 0.388 0.224
Cumulative Var 0.388 0.612
Factor Correlations:
Factor1 Factor2
Factor1 1.000 0.239
Factor2 0.239 1.000
Test of the hypothesis that 2 factors are sufficient.
The chi square statistic is 0.22 on 1 degree of freedom.
The p-value is 0.639
- Uniquenesses 는 유효성을 판단하는 값으로 통상 0.5 이하이면 유효함. 전체 변수 중 1개의 변수를 제외하고는 모두 0.5 이하의 값을 보이고 있다.
- 2개의 요인까지 나왔다. (factanal의 2번째 매개변수를 3으로 하면 3개의 공통요인을 찾으라는 건데, 더 많은 변수가 필요하다고 에러난다)
- Loadings가 요인 부하량인데..
- Factor1을 보면 청결상태, 대기시간, 친절 변수가 값이 0.5이상(보통 0.3 이상이면 유의하다고 봄)으로 크다.
- Factor2를 보면 음식맛 이 0.99로 굉장히 크다. 음식량은 0.37으로 값이 작다.
- Factor1을 보면 청결상태, 대기시간, 친절 변수가 값이 0.5이상(보통 0.3 이상이면 유의하다고 봄)으로 크다.
- Cumulative Var(설명되는 총분산의 누적값) - Factor2까지 0.612만큼 설명됨.
- Factor Correlations - Factor1와 Factor2는 별로 상관이 없다.
- p-value 0.639로 요인 분석은 귀무가설을 기각하지 못하므로, 요인분석은 유의미
- 귀무가설: 현재 추출된 요인이 측정 변수 사이의 관계를 정확히 설명함(차이 없음)
- 대립가설: 현재 추출된 요인보다 더 많은 요인이 필요(차이 있음)
- 귀무가설이 기각되면, 요인분석의 무의미함.
- 귀무가설: 현재 추출된 요인이 측정 변수 사이의 관계를 정확히 설명함(차이 없음)
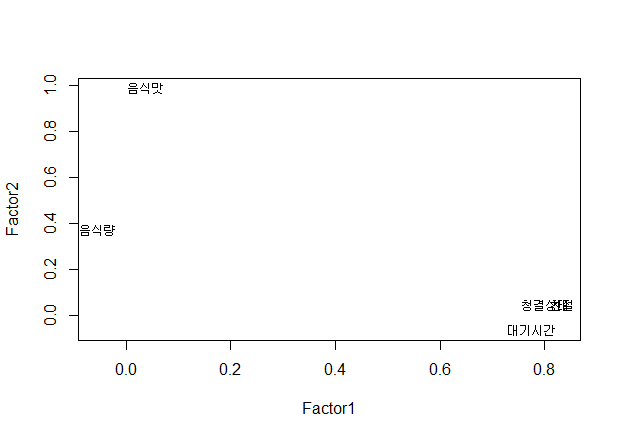
#요인회전을 안시키면 차트가 조금 다르게 나타남 #fit <- factanal(x, 2, rotation="none") load <- fit$loadings[,1:2] plot(load,type="n") # set up plot text(load,labels=names(x),cex=.7) # add variable names

factanal()함수가 에러 나면..
library(psych) library(GPArotation) fit <- fa(r=cor(x1), nfactors=3, rotate="promax") summary(fit) load <- fit$loadings[,1:2] plot(load,type="n") # set up plot text(load,labels=names(x),cex=.7) # add variable names
아래와 같이 하면 공통요인값을 구할 수 있다.
> factanal(x, 2, rotation="promax", scores="regression")$scores
Factor1 Factor2
[1,] 0.8266176 1.15483124
[2,] 0.5335642 1.24017288
[3,] 0.5908294 0.35575418
[4,] -0.3220569 -1.12270001
[5,] -0.5015774 -1.07468932
[6,] -1.0200758 -0.06511692
[7,] -1.1099463 -0.90967064
[8,] -0.9146350 -0.09589597
[9,] 1.0607151 0.22680194
[10,] 0.2550042 -0.41469562
[11,] -0.1482268 1.42528154
[12,] -1.0589853 -0.06032610
[13,] -0.8896313 0.76484419
[14,] 1.4105432 0.13182575
[15,] -0.3724041 -1.10981555
[16,] -0.4344594 0.63898395
[17,] -1.6638319 2.69963963
[18,] 1.2315831 0.18258979
[19,] 1.4379888 -1.60177959
[20,] 0.7387958 -1.40917884
[21,] -0.8238109 -0.12347804
[22,] -0.3307093 -1.11890147
[23,] -0.8399416 0.74910139
[24,] 1.0109283 0.24243975
[25,] 1.3337221 -0.70601818
![[-] [-]](/moniwiki/imgs/plugin/arrup.png)
![[+] [+]](/moniwiki/imgs/plugin/arrdown.png)
